class Vectex {
    public int Index;//代表该顶点的下标
    public Vectex(int index) {
        Index = index;
    }
}

class Edge {

    public Vectex From,To;
    public int Weight;

    public Edge(Vectex from, Vectex to,int weight) {
        From = from;
        To = to;
        Weight = weight;
    }
}

class Program
{
    static void Main(string[] args)
    {
                
        //构建图
        Vectex O = new Vectex(0);
        Vectex A = new Vectex(1);
        Vectex B = new Vectex(2);
        Vectex C = new Vectex(3);
        Vectex D = new Vectex(4);
        Vectex[] vectexs = new Vectex[] { O, A, B, C, D };

        Dictionary<Vectex, Edge[]> datas = new Dictionary<Vectex, Edge[]>();
        Edge OA = new Edge(O, A, 2);
        Edge OB = new Edge(O, B, 3);
        Edge AC = new Edge(A, C, 7);
        Edge AD = new Edge(A, D, -1);
        Edge BD = new Edge(B, D, 1);
        Edge DC = new Edge(D, C, 2);
        datas.Add(O, new Edge[] { OA, OB });
        datas.Add(A, new Edge[] { AC,AD });
        datas.Add(B, new Edge[] { BD });
        datas.Add(D, new Edge[] { DC });
        //构建图 结束

        int[] results = Ford(datas, vectexs);
        foreach (var ii in results) {
            Console.Write(ii + " ");
        }

        Console.ReadKey();
    }

    static int[] Ford(Dictionary<Vectex,Edge[]> datas, Vectex[] vectexs) {
        int vNum = vectexs.Length;
        int[] book = new int[vNum];
        int[] dis = new int[vNum];
                
        //初始化记录从原点到目标点的最短路径长度
        for (int i = 0; i < vNum; i++) {
            dis[i] = int.MaxValue;
        }
        dis[0] = 0;

        Queue<Vectex> queue = new Queue<Vectex>();
        queue.Enqueue(vectexs[0]);
        book[0] = 1;
            
        Vectex v;
        while(queue.Count>0){
            v = queue.Dequeue();
            Edge[] edges;
            datas.TryGetValue(v, out edges);
            book[v.Index] = 0;
            if (edges == null) {
                continue;
            }

            foreach (var e in edges) {
                if (dis[e.To.Index] > dis[v.Index] + e.Weight) {
                    //如果有需要，可以增加一个父节点记录数组，这样就可以通过目标点得到路径了
                    dis[e.To.Index] = dis[v.Index] + e.Weight;
                    if(book[e.To.Index == 0){
                      queue.Enqueue(e.To);
                      book[e.To.Index] = 1;
                    }
                }
            }
        }

        return dis;
    }
}

可以计算有负权值的图，这里计算了每一个点距离原点的最短距离。用一个队列来记录可能需要优化的顶点，还有一个book字典记录已经在队列中的顶点，防止同样的顶点再次进入队列，这样是没必要的。还有一个就是每个顶点距离原点的距离了。

首先初始化所有的值，队列，让原点进队。遍历队列的顶点，为每个顶点可到顶点寻找更短的路径，如果找到了，修改结果数组，把路径的结果顶点加入到队列中，因为它的值被改变了，可能会影响到它可到的顶点。当队列为空时，证明结果数组的路径都是最短路径了。

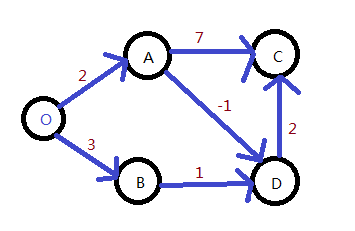结果：0,2,3,3,1