数据结构和算法
线性表的链式存储结构存储的元素的存储位置是可以不连续的,也就是说它们可以分布到各个地方,通过某种绳子把它们联系起来。
每个元素除了存储自己的数据外,还要拥有一条绳子链接上下一个元素。
链式存储结构的线性表没有空间的限制,存储的数据个数可以自由扩充。
class MyLink<T>
{
class Node
{
public T data;
public Node next;
}
private Node _head;
private Node _last;
private int _curentLinkLength;
//构造函数,创建头结点,空链表
public MyLink()
{
_head = new Node();
_head.next = null;
_last = _head;
this._curentLinkLength = 0;
}
}一个Node表示一个结点也就是一个数据,一个链表有一个头结点,用来方便插入元素到第一个等,头结点的下一个元素next就是第一个结点了,如果为null,那么就是空链表了。
last是新加的,方便在尾部添加新元素,而不用从头到尾遍历一遍,就是浪费了一定存储空间而已。
//通过索引删除元素
public T DeleteByIndex(int index) {
if (index < 1 || index > this._currentLength) {
Console.WriteLine("索引非法!");
return default(T);
}
T deleteData = this._data[index - 1];
for (int i = index - 1; i < this._currentLength - 1; i++) {
this._data[i] = this._data[i + 1];
}
this._currentLength--;
return deleteData;
}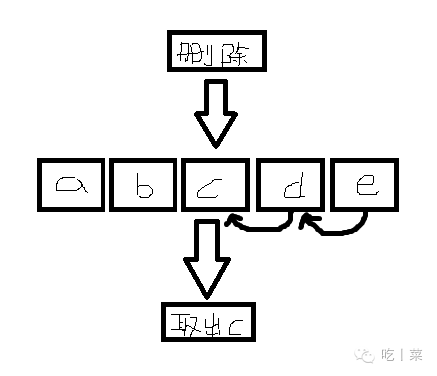
先检查要删除的位置有没有超过范围了,超过了你删条毛啊
将要删除位置的后面元素往前覆盖就删掉了
后面乜有元素?长度-1也是访问不到删除元素的了,也是删除了的意思
//插入元素
public bool Insert(int index, T element) {
if (index < 1 || index > this._currentLength) {
Console.WriteLine("索引非法!");
return false;
}
if (this._currentLength < this._maxLength) {
for (int i = this._currentLength-1; i >= index-1; i--) {
this._data[i + 1] = this._data[i];
}
this._data[index - 1] = element;
this._currentLength++;
return true;
}
Console.WriteLine("不能向已满的表插入元素!");
return false;
}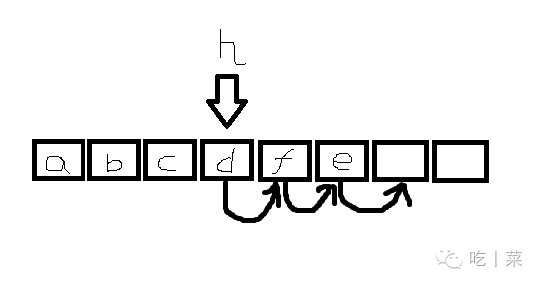
先检查插入位置是否合法,总不能一下子插入到数据域的末尾孤零零一个数据吧,这样数据就不连续了
然后检查数据有没有满,满了你还插啊,插哪里去啊
最后就是将插入位置空出来,插入位置后面的元素往后挪,挪完后坐下就好了,当然长度要加1了
//添加元素
public bool Add(T element)
{
if (this._currentLength < this._maxLength)
{
this._data[this._currentLength] = element;
this._currentLength++;
return true;
}
Console.WriteLine("元素已满!!");
return false;
}在判断不超过数组大小的情况下,就可以直接在数组(数据域)末尾元素后面位置添加上元素
长度+1
线性表就是有者0-多个数据元素组成的有限序列。
线性表规定了一个有限大小的数据域来保存数据,当然还有一个指标表示当前的数据元素的多少。
顺序存储结构对应的就是连续的存储空间,数据元素之间的存储是连续的。
class MyList<T>
{
private T[] _data;
private int _maxLength = 24;
private int _currentLength = 0;
public MyList()
{
this._data = new T[this._maxLength];
}
}
时间复杂度:用来衡量算法的运算时间。
衡量方法:用1代替所有+法的常数,保留次数最高的阶项,去除系数。
空间复杂度:运行算法时所需要的内存空间。
数据间存在多对多的关系。
每一个元素都可能存在有多个前驱和多个后继。
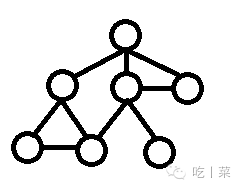
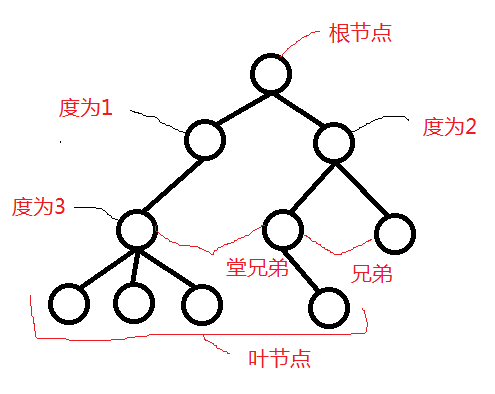
数据间存在一对多的关系。
排除根节点,每个数据的前驱只有一个。
排除叶节点,每个数据的后缀可以是1-n个。
数据元素之间有个一对一的关系,那么就连成了一个线性关系。
判定是否是线性关系,可以将头尾元素排除,看看每个元素是否有着唯一的前驱和后继。
每个数据除了同属于一个集合外,没有其他不三不四的关系了。
就像圆圈内的小点们,除了在同一个圆圈内,它们之间并没有其他的联系。
