读一读
计算机中乘法指令比除法指令要快，如果涉及大量的计算，这也是一种优化，养成这个习惯也能提高程序的性能。例如：
f = num / 2; f = num * 0.5f;
这两个表达式的运算结果是一样的，但是使用乘法指令会比较快。
class Vectex {
public int Index;//代表该顶点的下标
public Vectex(int index) {
Index = index;
}
}
class Edge {
public Vectex From,To;
public int Weight;
public Edge(Vectex from, Vectex to,int weight) {
From = from;
To = to;
Weight = weight;
}
}
class Program
{
static void Main(string[] args)
{
//构建图
Vectex O = new Vectex(0);
Vectex A = new Vectex(1);
Vectex B = new Vectex(2);
Vectex C = new Vectex(3);
Vectex D = new Vectex(4);
Vectex[] vectexs = new Vectex[] { O, A, B, C, D };
Dictionary<Vectex, Edge[]> datas = new Dictionary<Vectex, Edge[]>();
Edge OA = new Edge(O, A, 2);
Edge OB = new Edge(O, B, 3);
Edge AC = new Edge(A, C, 7);
Edge AD = new Edge(A, D, -1);
Edge BD = new Edge(B, D, 1);
Edge DC = new Edge(D, C, 2);
datas.Add(O, new Edge[] { OA, OB });
datas.Add(A, new Edge[] { AC,AD });
datas.Add(B, new Edge[] { BD });
datas.Add(D, new Edge[] { DC });
//构建图 结束
int[] results = Ford(datas, vectexs);
foreach (var ii in results) {
Console.Write(ii + " ");
}
Console.ReadKey();
}
static int[] Ford(Dictionary<Vectex,Edge[]> datas, Vectex[] vectexs) {
int vNum = vectexs.Length;
int[] book = new int[vNum];
int[] dis = new int[vNum];
//初始化记录从原点到目标点的最短路径长度
for (int i = 0; i < vNum; i++) {
dis[i] = int.MaxValue;
}
dis[0] = 0;
Queue<Vectex> queue = new Queue<Vectex>();
queue.Enqueue(vectexs[0]);
book[0] = 1;
Vectex v;
while(queue.Count>0){
v = queue.Dequeue();
Edge[] edges;
datas.TryGetValue(v, out edges);
book[v.Index] = 0;
if (edges == null) {
continue;
}
foreach (var e in edges) {
if (dis[e.To.Index] > dis[v.Index] + e.Weight) {
//如果有需要，可以增加一个父节点记录数组，这样就可以通过目标点得到路径了
dis[e.To.Index] = dis[v.Index] + e.Weight;
if(book[e.To.Index == 0){
queue.Enqueue(e.To);
book[e.To.Index] = 1;
}
}
}
}
return dis;
}
}可以计算有负权值的图，这里计算了每一个点距离原点的最短距离。用一个队列来记录可能需要优化的顶点，还有一个book字典记录已经在队列中的顶点，防止同样的顶点再次进入队列，这样是没必要的。还有一个就是每个顶点距离原点的距离了。
首先初始化所有的值，队列，让原点进队。遍历队列的顶点，为每个顶点可到顶点寻找更短的路径，如果找到了，修改结果数组，把路径的结果顶点加入到队列中，因为它的值被改变了，可能会影响到它可到的顶点。当队列为空时，证明结果数组的路径都是最短路径了。
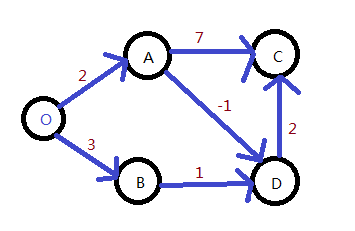结果：0,2,3,3,1
static int n;
static void Main(string[] args)
{
Console.WriteLine("输入1-9的数字");
n = Convert.ToInt32( Console.ReadLine());
dfs();
Console.ReadKey();
}
static int[] book = new int[10];//用来标志数有没被用
static int[] result = new int[10];//记录结果
static void dfs(int step = 1) {
if (step > n) {
foreach (var val in result) {
if (val != 0) {
Console.Write(val + " ");
}
}
Console.WriteLine();
return;//退出口
}
for (int i = 1; i <= n; i++) {
if (book[i] == 0) {//这个数字没被用，则用它
result[step] = i;
book[i] = 1;
dfs(step+1);
//从上一步回来了，取回这个数才能尝试下一个数
book[i] = 0;
}
}
}深度优先搜索的思想，先遍历到最尾处出现一种情况了再返回
递归的方式实现，其实就是栈的方式，涉及深度优先搜索的采用栈来解决
这种计算遍历了所有情况
static void Main(string[] args)
{
int[] datas = new int[100000];
for (int j = 0; j < 100000; j++) {
datas[j] = r.Next(1, 10000);
}
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
sortArray(0, datas.Length - 1, datas);
stopwatch.Stop();
foreach (int data in datas) {
Console.WriteLine(data);
}
Console.WriteLine("是否排序好：" + isSort(datas));
Console.WriteLine("运行时间:" + stopwatch.ElapsedMilliseconds);
Console.ReadKey();
}
static void sortArray(int start,int end,int[] datas) {
if (start >= end) {
return;
}
int i = start;
int j = end;
//左边参考值 ，从小到大排序
int refer = datas[start];
while (i != j) {
//先搜索比参考值小的
while (datas[j] >= refer && j > i)
{
j--;
}
while (datas[i] <= refer && i < j) {
i++;
}
if (i < j) {
//交换
int temp = datas[i];
datas[i] = datas[j];
datas[j] = temp;
}
}
//把参考值放到中间相撞位置
datas[start] = datas[i];
datas[i] = refer;
sortArray(start, i - 1, datas);
sortArray(i + 1, end, datas);
}
static bool isSort(int[] datas) {
for (int i = 0; i < datas.Length -1; i++) {
if (datas[i] > datas[i + 1]) {
return false;
}
}
return true;
}思想就是，先定一个参考值（左边参考值或右边参考值），这个左右边参考值涉及到先搜索比参考值小的还是比参考值大的。例如，先定一个左边参考值，从右边搜索比参考值小的，再从数据左边开始搜索比参考值大的，然后交换这两个值，一直到这两个搜索撞到了一起。而这个撞在一起的值，就是那个先搜索的（比参考值小），让参考值归为到中间，因为选取参考值时是选取的左边位置，所以，直接交换中间相撞位置和参考值位置就行了。同理的，选取右边参考的话，就要先搜索左边的，先搜索比参考值大的。
模拟排序10W条随机数据用时：20ms，快得飞起啊，而且空间复杂度也低
static void Main(string[] args)
{
int[] datas = new int[100000];
Random r = new Random();
for (int i = 0; i < 100000; i++) {
datas[i] = r.Next(1, 10000);
}
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
int[] newdatas = SortChoice(datas);
stopwatch.Stop();
foreach (int data in newdatas) {
Console.WriteLine(data);
}
Console.WriteLine("用时：" + stopwatch.ElapsedMilliseconds);
Console.ReadKey();
}
static int[] SortChoice(int[] datas)
{
int length = datas.Length;
int[] newArr = new int[datas.Length];
for (int x = 0; x < length; x++)
{
newArr[x] = datas[x];
}
int index = 0;
for (int i = 0; i < length; i++)
{
index = i;
for (int j = i + 1; j < length; j++)
{
if (newArr[j] < newArr[index])
{
index = j;
}
}
if (index != i) {
int temp = newArr[i];
newArr[i] = newArr[index];
newArr[index] = temp;
}
}
return newArr;
}原理其实跟冒泡排序是一样的，不同的是，选择排序减少了交换的次数，可以看出，代码中发现了更小的元素时，不是选择交换合适选择记录下来，最后的时候才判断需要需要交换再进行交换。
因为少了交换的步骤，效率会比冒泡排序的要快。
模拟排序10W条随机数据用时：16886ms
这个算法是归并算法的第二步根本所在，前面已经写过了
vector<int> mergeSortedArray(vector<int> &A, vector<int> &B) {
// write your code here
vector<int> res ;
int i = 0;
int j = 0;
//只需要比完一个数组中的元素
while(i<A.size()&&j<B.size()){
if(A[i]<B[j]){
res.push_back(A[i++]);
}else{
res.push_back(B[j++]);
}
}
//填充剩下的元素到后面
while(i<A.size()){
res.push_back(A[i++]);
}
while(j<B.size()){
res.push_back(B[j++]);
}
return res;
}这里是c++描述，合并需要考虑两个数组相差很大的情况，所有只需要比较一个数组中的所有元素
剩下的直接填充进去了，剩下的也必然比另外一个用完的大，所以，排序好了
static void Main(string[] args)
{
int n = 12;
Int64 sum = 1;
for (int i = 1; i <= n; i++) {
sum *= i;
}
Console.WriteLine("结果:" + sum);
Console.WriteLine(cal(n));
Console.ReadKey();
}
static int cal(int n) {
int temp = n;
int count = 0;
while (temp != 0) {
temp = temp / 5;
count += temp;
}
return count;
}在阶乘中，出现凡是出现5的都会与偶数化简的2相乘变成10，从而尾部就多了一个0。
例如25的阶乘，
1-4都没有5，这里0个，
5可以和2变成10，所以这里1个，
6-9，不可以化出5，
10=2*5，这里1个5，所以1个，
15=3*5,1个，
20=4*5，一个，
25=5*5，注意了，这里就有2个了，两个5可以和偶数组合成两个10相乘
所以25 = 2+1+1+1+1 = 6个0
可以化简成 25/5 + 25/5/5 = 6。
公式为：n/5 + n/5/5 + ... + 0
桶排序是一种快速排序的算法。也是一种采用分治思想的算法。主要思路就是将所有的数据根据大小的不同放到不同的桶当中，桶从小到大排列，对每个桶里面的元素进行排序后，再合并桶就完成排序了。
static void Main(string[] args)
{
//构造10w条随机的数据
Random r = new Random();
int[] datas = new int[100000];
for (int i = 0; i < 100000; i++) {
datas[i] = r.Next(1, 100000);
}
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
List<int> res = TongSort(datas);
stopwatch.Stop();
foreach (var data in res) {
Console.WriteLine(data);
}
Console.WriteLine("用时:" + stopwatch.ElapsedMilliseconds);
Console.ReadKey();
}
static List<int> TongSort(int[] datas) {
int length = datas.Length;
//根据数据长度计算桶的数量
int num = (int)Math.Log(length) + 1;
List<int>[] lists = new List<int>[num];//新建这么多个桶
//初始化桶
for (int init = 0; init < lists.Length; init++) {
lists[init] = new List<int>();
}
//确定区间，用最大和最小值
int min = 0, max = 0;
for (int i = 0; i < length; i++) {
if (min > datas[i])
{
min = datas[i];
}
else {
if (max < datas[i])
max = datas[i];
}
}
int section = (max - min) / num + 1;
int index = 0;
foreach (int data in datas) {
//确定元素，属于哪个桶的下标，添加到桶里
index = data / section;
lists[index].Add(data);
}
List<int> result = new List<int>();
//对所有桶分别排序，再合并
for (int j = 0; j < lists.Length; j++) {
lists[j].Sort();//不知道是不是快排
result.AddRange(lists[j]);
}
return result;
}对10w条随机数据的排序需要时间:9-11ms
跳跃表是一个对链表结构的扩展，快速查找到有序链表结点。对于链表，如果要查找某一个结点，这时候就要对链表进行一个一个的比较，这时候的时间复杂度就是O（n）。速度其实不算慢了，但是有没有更加快速的方法呢。就跟查询表数据那样，有几千万数据时，查询一条数据，需要一条一条来对比，这不就炸了吗？那么数据库是怎么解决的？就是用的索引了。在链表上建立一层一层的链表，存储对应索引或结点的引用，根据查找的数据，在第一层索引确定范围，然后第二层...到数据层链表，之后只需要沿着链表对比少量结点就能找到了。插入结点时，对节点做循环随机50%的几率升层作为索引，能上几层就几层。删除结点，删除相应对应的引用了的索引。
参考：什么是跳跃表？
static void Main(string[] args)
{
//随机10W个数据
int[] datas = new int[100000];
Random r = new Random();
for (int i = 0; i < 100000; i++) {
datas[i] = r.Next(1,10000);
}
Stopwatch stopwatch = new Stopwatch();
stopwatch.Start();
sort(datas);//排序
stopwatch.Stop();
foreach (var data in datas) {
Console.WriteLine(data);
}
Console.WriteLine();
Console.WriteLine("用时：" + stopwatch.ElapsedMilliseconds);
Console.ReadKey();
}
static void sort(int[] datas) {
int length = datas.Length;
int[] temp = new int[length];
sort(datas, 0, length - 1, temp);
}
static void sort(int[] datas,int left,int right,int[] temp) {
if (left < right) {
int mid = (left + right)/2;
//拆分
sort(datas, left, mid, temp);
sort(datas, mid + 1, right, temp);
//合并，拆到不能拆就合并
merge(datas, left, mid, right, temp);
}
}
static void merge(int[] datas, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
int t = 0;
//对比左右两边（两边都已经是有序的了，所以从左往右对比）,排序(谁小先)填充到临时数组
while (i <= mid && j <= right) {
if (datas[i] < datas[j])
{
temp[t++] = datas[i++];
}
else {
temp[t++] = datas[j++];
}
}
//填充剩下了
while (i <= mid) {
temp[t++] = datas[i++];
}
while (j <= right) {
temp[t++] = datas[j++];
}
//将排序好的临时数据覆盖到原来的数组中
t = 0;
while (left <= right) {
datas[left++] = temp[t++];
}
}思想：将数据一直对半分组，分到组的数据都排序好为止(1个数据肯定是排序好的)，再将相邻的组合并起来（边合并，边排序），合并成的组又是一个排序好的组。
时间复杂度：O(nlogn)
10W个随机数据排序用时：33ms
稳定而又快速的排序方法，参考：dreamcatcher-cx（归并排序）