class ShellSort
{
public bool Sort(int[] datas)
{
if (datas.Length < 1) return false;
for (int gap = datas.Length / 2; gap > 0; gap /= 2)
{
for (int i = gap; i < datas.Length; i++)
{
//gap将集合分成几个小集合，跨着对比交换，最后gap=1时，减轻大集合的负担
int j = i;
while (j - gap >= 0 && datas[j] < datas[j - gap])
{
//当前集合的对比，让每个跨越式的小集合都是有序的
swap(datas, j, j - gap);//交换两个数的值
j -= gap;
}
}
}
return true;
}
private void swap(int[] data, int a, int b)
{
data[a] = data[a] + data[b];
data[b] = data[a] - data[b];
data[a] = data[a] - data[b];
}
}希尔排序是在插值排序中升级的，将数组改成几个大间距的不同集合，对这些集合进行交换的排序。交换大范围的数据，当在gap缩小到1的时候，就是插值排序了，这时候序列在前面大范围的比较交换后已经有了一定的顺序了，所以只需要交换少量数据就可以完成排序了。
测试代码：
static void TestShellSort()
{
int[] datas = { 5, 6, 9, 1, 100, 3, 7, 0, 2 };
ShellSort shellSort = new ShellSort();
shellSort.Sort(datas);
foreach (var data in datas)
{
Console.Write(data + " ");//0 1 2 3 5 6 7 9 100
}
}
class InsertSort
{
public bool Sort(int[] datas)
{
if (datas.Length < 1) return false;
for (int i = 1; i < datas.Length; i++)//默认0为已经有序
{
int temp = datas[i];//当前需要插入的元素
for (int j = 0; j < i; j++)//在有序段中寻找位置
{
if (temp < datas[j])//寻找到
{
for (int k = i; k > j; k--)
{
datas[k] = datas[k - 1];//向后面腾出位置
}
datas[j] = temp;//坐上宝座
break;
}
}
}
return true;
}
}插入排序就是将数组分为了左右两个集合，一个是有序的，一个是无序的，从无序中每次取一个元素，插入到有序的集合中，并保持有序。算法的效率是O(n2)，不适合大量元素的排序。
测试代码：
static void TestInsertSort()
{
int[] datas = { 5, 6, 9, 1, 100,3, 7, 0, 2, 4 };
InsertSort insertSort = new InsertSort();
insertSort.Sort(datas);
foreach (var data in datas)
{
Console.Write(data + " ");//0 1 2 3 4 5 6 7 9 100
}
}
对于平衡二叉树的删除方法是一样需要照顾平衡二叉书的平衡的，删除结点会导致bf的值改变，对于不平衡的需要平衡一下。
static bool DeleteElement(ref Node node, int data, ref bool lower)
{
bool L = false, R = false;
if (node == null) return false;
if (node.data == data)
{
Node p, s;
p = node.cRight;
s = p;
lower = true;
if (node.cRight == null)
{
p = node;
node = node.cLeft;//右边为空，直接把左边替换上去
lower = true;
return true;
}
else
{
while (s != null)
{
p = s;//找到的最左结点
s = s.cLeft;
}
node.data = p.data;//替换数据，引用保留
DeleteElement(ref node.cRight, data, ref lower);//删除那个最小结点
R = true;//往右走
}
}
else if (data < node.data)
{
DeleteElement(ref node.cLeft, data, ref lower);
L = true;
}
else
{
DeleteElement(ref node.cRight, data, ref lower);
R = true;
}
if (lower)
{
if (L)
{
switch (node.bf)
{
case LH:
node.bf = EH;
lower = true;
break;
case RH://本来右边高了，又删了个左边，所以要右平衡一下
RightBalance(ref node);
lower = false;
break;
case EH:
node.bf = RH;
lower = false;
break;
}
}
else
{
switch (node.bf)
{
case EH:
node.bf = LH;
lower = false;
break;
case RH:
node.bf = EH;
lower = true;
break;
case LH:
LeftBalance(ref node);
lower = false;
break;
}
}
}
return true;
}采用递归的方式，同样的有一个标志位lower来去判断是否需要平衡的检查。删除结点的操作是一样的，发现小的数据往左边，发现大的往右边，当相等的时候就是要删除的数据了。
同样分两种情况，右边为空，则直接将左边结点替换根。如果右边不为为空，则找到右边的最小(左)结点，替换调根的数值但保留根的左右结点，再删除最小结点。
平衡判断也是看情况的，比如说本来右边高的1，然后把左边删了，那就不平衡了，需要右平衡调整一下。
static void LeftBalance(ref Node node)
{
Node L, lr;
L = node.cLeft;
switch (L.bf)
{
case EH:
L.bf = RH;
node.bf = LH;
R_Rotate(ref node);
break;
case LH:
L.bf = node.bf = EH;
R_Rotate(ref node);
break;
case RH:
lr = L.cRight;
switch (lr.bf)
{
case EH:
L.bf = L.bf = EH;
break;
case RH:
node.bf = EH;
L.bf = LH;
break;
case LH:
L.bf = EH;
node.bf = RH;
break;
default:
break;
}
lr.bf = EH;
L_Rotate(ref node.cLeft);
R_Rotate(ref node);
break;
}
}解析的话 参考平衡二叉树的右平衡方法
//右平衡,右边高了
static void RightBalance(ref Node node)
{
Node R, r1;
R = node.cRight;
switch (R.bf)
{
case RH:
//右孩子和它一样的平衡因子，直接右旋转
node.bf = EH;
R.bf = EH;
L_Rotate(ref node);
break;
case EH:
node.bf = RH;
R.bf = LH;
L_Rotate(ref node);
break;
case LH:
r1 = R.cLeft;
switch (r1.bf)
{
case EH:
node.bf = EH;
R.bf = EH;
break;
case RH:
R.bf = EH;
node.bf = LH;
break;
case LH:
R.bf = RH;
node.bf = EH;
break;
}
r1.bf = EH;
R_Rotate(ref node.cRight);
L_Rotate(ref node);
break;
}
}
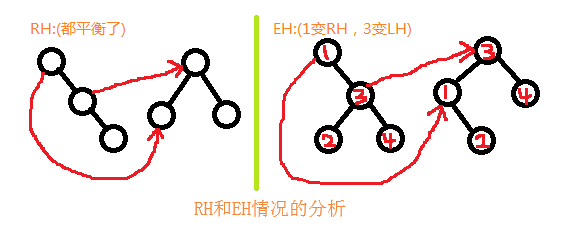
看情况，旋转之后的bf状态值会有所改变，所以要具体分析到每一种情况之下。
LH的情况比较多样这里就不详细分析了，不过要讲它为啥要先左旋其右结点再右旋自己。看图：
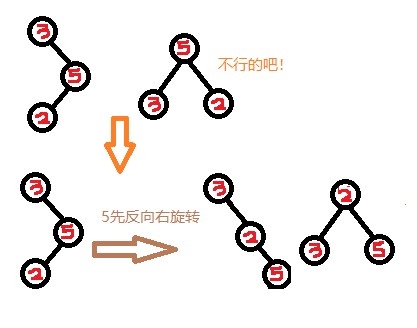
这种情况就是右平衡的时候，其子树的bf方向是不一致的，需要反向调整到一致，不然就不是一个排序树了。
static bool InsertAVLTree(ref Node node, int data, ref bool taller)
{
if (node == null)
{
node = new Node();
node.bf = EH;
node.data = data;
taller = true;
return true;
}
else {
if (data == node.data)
{
taller = false;
return false;
}
if (data < node.data)
{
if (!InsertAVLTree(ref node.cLeft, data, ref taller))
{
return false;
}
if (taller)
{
switch (node.bf)
{
case EH:
node.bf = LH;
taller = true;
break;
case LH:
LeftBalance(ref node);
taller = false;
break;
case RH:
node.bf = EH;
taller = false;
break;
default:
break;
}
}
}
else
{
if (!InsertAVLTree(ref node.cRight, data, ref taller))
{
return false;
}
if (taller)
{
switch (node.bf)
{
case EH:
node.bf = RH;
taller = true;
break;
case LH:
node.bf = EH;
taller = false;
break;
case RH:
RightBalance(ref node);
taller = false;
break;
default:
break;
}
}
}
}
return true;
}使用递归的方式，使用一个taller标识符来确认是否需要去判断要不要进行检查平衡操作。
插入成功之后，就设为true,然后程序玩下执行判断是否需要进行平衡操作，这里讲一下左插入的操作，右边的差不多。
当左插入成功后，就判断原结点的bf值，根据不同情况不同处理：
是EH时，表示当前结点下是平衡的，插入了一个左边的值，则让bf=LH就行了，taller设为true往上传递
是LH时，表示在左边高的时候又加了一层，则需要左平衡一下，平衡完后taller就为false
是RH时，表示右边高的时候在左边加了一层，那不就平衡了吗，设bf为EH，taller也为false
在进行平衡二叉树的构建构成中，每当发现不平衡的结点就要及时的做平衡。根据不同的情况对最小不平衡子树进行左右旋转操作。例如：（左旋转）
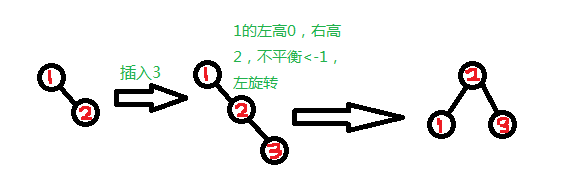
右边多的进行左旋转，把1拉下来，看起来想往左边转吧！
//左旋转
static void L_Rotate(ref Node node)//传入的是1
{
Node temp;
temp = node.cRight;
node.cRight = temp.cLeft;//2的左结点设为给1的右节点
temp.cLeft = node;//2的左边设为1
node = temp;//原1的位置改为2，这解释，啧啧
}node.cRight = temp.cLeft;-》如果说原来2是有左结点的话设为x，x<2，又2是1的右结点，所有1<x，又1的原右结点被破坏了，所以可以用1的右节点来承接x结点。如果不这样做的话，你试试，2有左右结点，然后一转，嘿嘿，三个结点了真是奇怪。
//右旋转
static void R_Rotate(ref Node node)
{
Node temp;
temp = node.cLeft;
node.cLeft = temp.cRight;//原前驱，变左结点
temp.cRight = node;
node = temp;
}右旋转和左旋转差不多，不同的是操作左右结点的不同。
平衡二叉树就是一颗排序二叉树，只不过比排序二叉树又多了一个条件，那就是每一个结点的左子树的高和右子树的高的差的绝对值（bf值）不能超过1，这样就可以解决一些排序二叉树不效率的问题了。
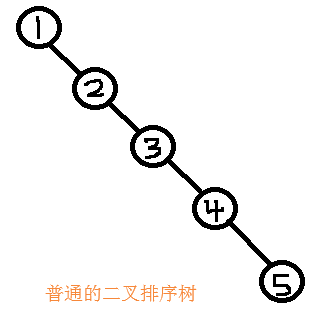
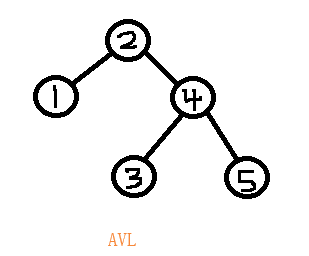
第一张图很明显的二叉排序树的优势就完全没有了，变成了普通的线性遍历搜索了。但是他变形成为一颗AVL平衡二叉树后，明显的效率就提高了，例如查找5，AVL3次，第一张的5次。
const int EH = 0;
const int LH = 1;
const int RH = -1;
class Node {
public int data;
public int bf;
public Node cLeft;
public Node cRight;
}平衡二叉树AVL的结点，每个结点都保存着一个bf值，就是它左子树-右子树的值的状态。
三个const表示，EH相等,LH左边高1，RH右边高1，没有出现高2的，因为有的话就会去平衡它了。
左右旋转操作：→
左平衡：→
插入操作：→
删除操作：→
完整的代码可以看：Github
二叉排序树的构建和插入在这里，请先看这个再看查找和删除。
static void Search(Node head,int data,ref Node targetNode, ref Node preNode)
{
//查找方法很简单
targetNode = head;
preNode = null;
while (targetNode != null && targetNode.data != data)
{
preNode = targetNode;
if (data < targetNode.data)
{
targetNode = targetNode.cLeft;
}
else
{
targetNode = targetNode.cRight;
}
}
}
//删除
static void Delete(ref Node head, int data)
{
Node targetNode = null;
Node preNode = null;
Search(head, data, ref targetNode, ref preNode);
if (targetNode == null) return;
if (targetNode.cLeft == null || targetNode.cRight == null)
{
//有一边的结点为空或两边都空，直接删调
Node tempTargetNode;
if (targetNode.cLeft == null)
{
tempTargetNode = targetNode.cRight;
}
else
{
tempTargetNode = targetNode.cLeft;
}
if (preNode == null)
{
head = tempTargetNode;
return;
}
if (preNode.cLeft == targetNode)//左边
{
preNode.cLeft = tempTargetNode;
}
else
{
preNode.cRight = tempTargetNode;
}
}
else
{
//两边都有
//在左边找一个最大的替换,就是目标的前驱。或则找后继，就是右边中最小的
Node LeftBig = targetNode.cLeft;
Node preBig = targetNode;
while (LeftBig.cRight != null)
{
preBig = LeftBig;
LeftBig = LeftBig.cRight;
}
preBig.cLeft = LeftBig.cLeft;//删除替换的节点，对接最大节点的左子树
//对接目标节点的左右子树
if (LeftBig != targetNode.cLeft)//排除特殊情况
{
LeftBig.cLeft = targetNode.cLeft;
}
LeftBig.cRight = targetNode.cRight;
if (preNode == null)
{
head = LeftBig;
return;
}
if (preNode.cLeft == targetNode)//左边
{
preNode.cLeft = LeftBig;
}
else
{
preNode.cRight = LeftBig;
}
}
}删除节点时，需要通过查找得到删除的节点和它的父节点。在删除节点下面的子节点中找一个替换他自己的节点，一个就是前驱一个就是后继了。这里考虑的是前驱。
分两种情况：
一种是，目标节点只有一个或没有子节点没有，只需要将存在的子节点替换掉目标节点就行了，因为但从一边的子树来讲本身就是一个完整的有序的。
另一种是，左右都存在的，直接需要找到前驱了，遍历左子树的右结点，找到最大的节点，移除这个最大的节点，注意这个节点可能存在的左子树要对接上它的父节点。然后将目标节点替换成这个最大的节点，也要注意对接上左右子树。
二叉排序树就是在一棵树中，满足每个结点的左子树结点都比它小，右子树结点比它大。
class Program
{
class Node
{
public int data;
public Node cLeft;
public Node cRight;
}
static void Main(string[] args)
{
int[] datas = { 9,2,6,3,1,22,8,55,77,33 };
Node head = null;
CreateOrderTree(ref head, datas);
PrintMid(head);//1 2 3 6 8 9 22 33 55 77
Console.ReadKey();
}
static void CreateOrderTree(ref Node head, int[] datas)
{
if (datas.Length < 1) return;
for (int i = 0; i < datas.Length; i++)
{
Insert(ref head, datas[i]);
}
}
//插入
static void Insert(ref Node head, int data)
{
if (head == null)
{
head = new Node();
head.data = data;
return;
}
Node temp = head;
Node preTemp = temp;
bool isLeft = false;
while (temp != null)
{
preTemp = temp;//访问到的最后一个节点，temp是空的
if (data < temp.data)
{
//左边
isLeft = true;
temp = temp.cLeft;
}
else if (data > temp.data)
{
isLeft = false;
temp = temp.cRight;
}
else
{
//重复的数据
return;
}
}
Node node = new Node();
node.data = data;
if (isLeft)
{
preTemp.cLeft = node;
}
else
{
preTemp.cRight = node;
}
}
//中序遍历输出
static void PrintMid(Node node)
{
if (node == null) return;
PrintMid(node.cLeft);
Console.Write(node.data + " ");
PrintMid(node.cRight);
}
}创建一个二叉排序树主要时调用插入方法构建而成的，所以主要的是插入方法，插入方法很简单，都是从树的根开始，每次从根部对比元素，小的往左走，大的往右走，直到为空位置，而这个空的位置就是该元素的位置，所有要保留一个PreNode就是最后访问到的节点和一个左右的标志，好确定新加的元素是最后节点的左还是右子节点。
需要注意的就是树为空的时候，直接跟根赋值就行了。